صيغ معادلة المستقيم - الرياضيات 1-1 - أول ثانوي

2-5 صيغ معادلة المستقيم Equations of Line فيما سبق درست إيجاد ميل المستقيم. الدرس (4-2) والان لماذا؟ قدمت إحدى شركات الاتصالات عرضًا يدفع بموجبه المشترك 30 ريالًا شهريًا بالإضافة إلى 0.30 ريال عن كل دقيقة اتصال. فإذا رمزنا للتكلفة الشهرية بالرمز C ، ولعدد دقائق الاتصال بالرمز t ، عرض شركة الاتصالات C = 0.3t + 30 رابط الدرس www.ien.edu.sa 80 60 40 20 20 التكلفة (ريال) أكتب معادلة مستقيم إذا عرفتُ معلومات حول تمثيله البياني. أحل مسألة بكتابة معادلة مستقيم. المفردات: صيغة الميل والمقطع slope-intercept form صيغة الميل ونقطة slope-point form فإن: C = 0.3t + 30 40 80 60 120 100 140 160 عدد دقائق الاتصال 0 20 كتابة معادلة المستقيم : تذكر أنه يمكن كتابة معادلة المستقيم بصيغ مختلفة، ولكنها متكافئة. مفهوم أساسي معادلة المستقيم غير الرأسي صيغة الميل والمقطع لمعادلة المستقيم هي y = mx + b ، حيث ميل المستقيم، و b مقطع المحور y = 3 x + 8 y صيغة الميل ونقطة لمعادلة المستقيم هي (1) - y - y = (x، حيث ( 1 ) إحداثيا أي نقطة على المستقيم ، m ميل المستقيم. الميل مقطع المحور ا أضف إلى مطويتك y = mx + b نقطة على المستقيم (3) ', y-5=-2 (x — 3) - الميل إذا علمت الميل ومقطع المحور y أو نقطة على المستقيم، فإنه يمكنك استعمال هاتين الصيغتين لتكتب معادلة المستقيم. مثال 1 معادلة المستقيم بصيغة الميل والمقطع اكتب بصيغة الميل والمقطع معادلة المستقيم الذي ميله ،3، ومقطع المحور y له 2- ، ثم مثله بيانيا. y = mx + b y=3x+(-2) y = 3x - 2 صيغة الميل والمقطع m = 3, b = -2 بسط 3 على المستوى الإحداثي، عيّن نقطة مقطع المحور ل عند 2- = y ، واستعمل قيمة الميل = = 3 لتحدد نقطة أخرى، وذلك بالانتقال 3 وحدات أعلى مقطع المحور ، ثم وحدة واحدة إلى يمينه ارسم المستقيم الذي يمر بهاتين . النقطتين. تحقق من فهمك 0 x | y = 3x - 2 1 اكتب بصيغة الميل والمقطع معادلة المستقيم الذي ميله ، ومقطع المحور y له 8 ، ثم مثله بيانيًا. الدرس - صيغ معادلة المستقيمة ال117م Ministry of Education 2024-1446

معادلة المستقيم غير الرأسي

معادلة المستقيم بصيغة الميل والمقطع

اكتب بصيغة الميل والمقطع معادلة المستقيم الذي ميله 1/2

أكتب معادلة مستقيم إذا عرفت معلومات حول تمثيله البياني

تنبيه ! التعويض بإحداثيات سالبة عند التعويض بإحداثيات سالبة، استعمل الأقواس لتتجنب الوقوع في أخطاء الإشارات. إرشادات للدراسة طريقة بديلة في المثال 36، يمكنك تعويض إحداثيي إحدى النقطتين في صيغة الميل والمقطع لإيجاد مقطع المحور y ، ثم كتابة المعادلة. مثال 2 معادلة المستقيم بصيغة الميل ونقطة (-2,5) اكتب بصيغة الميل ونقطة معادلة المستقيم الذي ميله ه ه - ، و ، ويمر بالنقطة (2) ، ثم مثله بيانيا. y - y1 = m(x - (1) 3 y-5=-³ [x-(-2)] 4 3 y - 5 = - f ( x + 2) 4 عين النقطة (2) في المستوى الإحداثي. صيغة الميل ونقطة 3 m= −1, (x1,y1) = (−2, 5) 4 بسّط واستعمل قيمة الميل = = - - لتحدد نقطة أخرى؛ وذلك بالانتقال -3 3 4 4 6. 3 وحدات أسفل النقطة (2) ، ثم 4 وحدات إلى يمينها. ارسم المستقيم المار بهاتين النقطتين. تحقق من فهمك (2) اكتب بصيغة الميل ونقطة معادلة المستقيم الذي ميله 4 ، ويمر بالنقطة (36) ، ثم مثله بيانياً. |y-5=-3 / (x+2) 4 x A 0 عندما لا يُعطى ميل المستقيم، استعمل أي نقطتين عليه لحساب ميله ، ثم استعمل صيغة الميل ونقطة، أو الميل والمقطع لتكتب معادلته. مثال 3 معادلة المستقيم المار بنقطتين معلومتين (0,3), (-2, -1) (a اكتب بصيغة الميل والمقطع معادلة المستقيم المار بكل زوج نقاط فيما يأتي: الخطوة 1 : أوجد ميل المستقيم المار بالنقطتين. y = mx + b 4 = = -1/2 (-7)+b 4 = 7 + b 4 4721 b = 2 - = b || || لذا 1 + y = - x 118 الفصل 2 التوازي والتعامد m = 92 - 91 X2 - 1 = -2-0 -1-3=-4=2 الخطوة 2: اكتب معادلة المستقيم. صيغة الميل والمقطع y = mx + b b = 3، m = 2 y = 2x + 3 (-7, 4), (9,-4) (b الخطوة 1: الخطوة 2 : تحقق من فهمك m= 92 - 91 X2 - 1 = -4-4 9- (-7) y-y₁ = m(x-x1) = -8 ― = 16 y - 4 = - [x - (-7)] 1 y - 4 = - = (x + 7) (-2, 4), (8, 10) (3A استعمل صيغة الميل استعمل صيغة الميل صيغة الميل ونقطة m=- 2 1, (x₁, y₁) = (−7, 4) بسط بالتوزيع اجمع 4 لكلا الطرفين y - 4 = - - x - 2 7 - y = - = x + 2 (0,0), (2,6) (3B وزارة التعليم Ministry of Education 2024-1446

مثال 2معادلة المستقيم بصيغة الميل ونقطة

معادلة المستقيم المار بنقطتين معلومتين

اكتب بصيغة الميل ونقطة معادلة المستقيم الذي ميله 4 ويمر بالنقطة (-3،-6) ثم مثله بيانيا

3A- اكتب بصيغة الميل والمقطع معادلة المستقيم المار بكل زوج نقاط فيما يأتي

مثال 4 معادلة المستقيم الأفقي اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يمر بالنقطتين (2) . الخطوة 1: الخطوة 2 : m = 92 - 91 x2-x1 = 6-6 5-(-2) = 0 y - y = m (x - 1 ) y - 6 = 0 [x-(-2)] y - 6 = 0 y = 6 تحقق من فهمك صيغة الميل ونقطة m = 0, (x1,y1) = (-2,6) بسط اجمع 6 لكلا الطرفين (4) اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يمر بالنقطتين (30) . تحتوي معادلات المستقيمات الأفقية أو الرأسية متغيرًا واحدًا فقط . مفهوم أساسي و أضف إلى معادلات المستقيمات الأفقية أو الرأسية مطويتك معادلة المستقيم الأفقي هي y = b ، Ay حيث b مقطع المحور y له. مثال : y = -3 معادلة المستقيم الرأسي هي x = a ، حيث a مقطع المحور x له. مثال : x = -2 x = - 2 0 x y = -3 المستقيمات المتوازية غير الرأسية لها الميل نفسه ويكون المستقيمان غير الرأسيين متعامدين إذا كان ناتج ضرب ميليهما يساوي 1- . والمستقيم الرأسي والمستقيم الأفقي دائمًا متعامدان. مثال 5 معادلات المستقيمات المتوازية أو المتعامدة اكتب بصيغة الميل والمقطع معادلة المستقيم العمودي على 2 + 3 = y ، والمار بالنقطة (40) ميل المستقيم 2 + y = −3x يساوي 3- ؛ لذا فإن ميل المستقيم العمودي عليه يساوي . صيغة الميل والمقطع y = mx + b 3 m = } , (x, y) = (4, 0) 0 = } (4) + b 0 = + b 3 - 1 = b بسّط اطرح و من كلا الطرفين لذا فمعادلة المستقيم العمودي هي ( ) + y = } x ، أو { 1 - y = 3 x. ) تحقق من فهمك 3 4 (5) اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يوازي 3 + x - = y ويمر بالنقطة (36) . الدرس - صيغ معادلة المستقيمة ال119م Ministry of Education 2024-1446

معادلة المستقيم الأفقي

معادلات المستقيمات الأفقية أو الرأسية

معادلات المستقيمات المتوازية أو المتعامدة

اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يمر بالنقطتين (0،3)، (0،5)

اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يوازي

قراءة الرياضيات خطي كلمة منسوبة إلى خط، وتتضمن معنى الاستقامة. وسميت المعادلات الخطية بهذا الاسم؛ لأن تمثيلها البياني خط مستقيم. كتابة معادلات لحل المسائل: يمكن تمثيل كثير من المواقف الحياتية باستعمال معادلة خطية. مثال 6 من واقع الحياة كتابة معادلة خطية هواتف يقارن علي بين عرضين مقدمين من شركة اتصالات. يدفع بموجب العرض X مبلغ 20 ريالا شهريًا بالإضافة إلى 0.35 ريال عن كل دقيقة اتصال. أما العرض X فتفاصيله موضحة في فقرة "لماذا؟" في بداية الدرس. أي العرضين أفضل لعلي؟ افهم : خطط حل العرض X : 20 ريالًا شهريًا زائد 0.35 ريال عن كل دقيقة اتصال. العرض : 30 ريالًا شهريًا زائد 0.30 ريال عن كل دقيقة اتصال. قارن بين العرضين لتحدد متى تكون التكلفة الشهرية لأحدهما أقل من التكلفة الشهرية للآخر. اكتب معادلة تمثل التكلفة الشهرية C لكلّ من العرضين لعدد t من دقائق الاتصال، ثم مثل المعادلتين بيانيا وقارن. معدلا التزايد أو ميلا معادلتي التكلفة الشهرية هما 0.35 للعرض X و 0.30 للعرض X، وعندما يكون عدد دقائق الاتصال صفرًا ، تكون التكلفة الشهرية هي الرسوم فقط ؛ لذا فإن مقطع المحور ا هو 20 للعرض X ، و 30 للعرض X . العرض Y C = mt + b C = 0.30t + 30 التكلفة ( ريال ) 100 90 90 00 80 70 70 60 60 50 40 30 صيغة الميل والمقطع بالتعويض عن m و b عروض شركة الاتصالات C = 0.30t + 30 20 | C = 0.35t + 20 10 0 20 60 40 80 العرض X C = mt + b C = 0.35t + 20 إرشادات حل المسألة التمثيل البياني في المثال 6 ، مع أن الرسوم الشهرية في سعر العرض X أقل، إلا أن دقيقة الاتصال الواحدة أعلى. وهذا يجعل المقارنة بين يظهر من التمثيل البياني أن تكلفتي العرضين تتساويان عندما يكون عدد دقائق الاتصال 200 دقيقة، وعندها تكون التكلفة 90 ريالا . 100 120 140 160 180 200 220 عدد دقائق الاتصال العرضين صعبة. إلا أن التمثيل البياني يُسهل المقارنة بين موقفين خطيين في كثير من الأحيان. ويظهر أيضًا من التمثيل البياني أنه إذا كان عدد دقائق الاتصال أقل من 200 دقيقة في الشهر ، فإن تكلفة العرض X أقل، بينما تكون تكلفة العرض X أقل إذا كان عدد دقائق الاتصال أكثر من 200 دقيقة في الشهر. تحقق : تحقق من تقديرك. إذا كان عدد دقائق الاتصال يساوي 200 دقيقة ، فإن تكلفة العرض. 90 = 20 + (200)0.35 ، وتكلفة العرض Y هي تحقق من فهمك (6) وضع نادي عرضين مختلفين لرواده :X 0.30(200) + 30 = 90 العرض :x: رسوم اشتراك شهرية مقدارها 75 ريالا زائد 20 ريالا عن كل زيارة للنادي. العرض : 35 ريالا عن كل زيارة للنادي من دون رسوم اشتراك. فأيُّ العرضين أفضل؟ X هي وزارة التعليم Ministry of Education 2024-1446 الفصل 2 التوازي والتعامد 120

كتابة معادلة خطية

التمثيل البياني

وضع نادي عرضين مختلفين لرواده أي العرضين أفضل؟

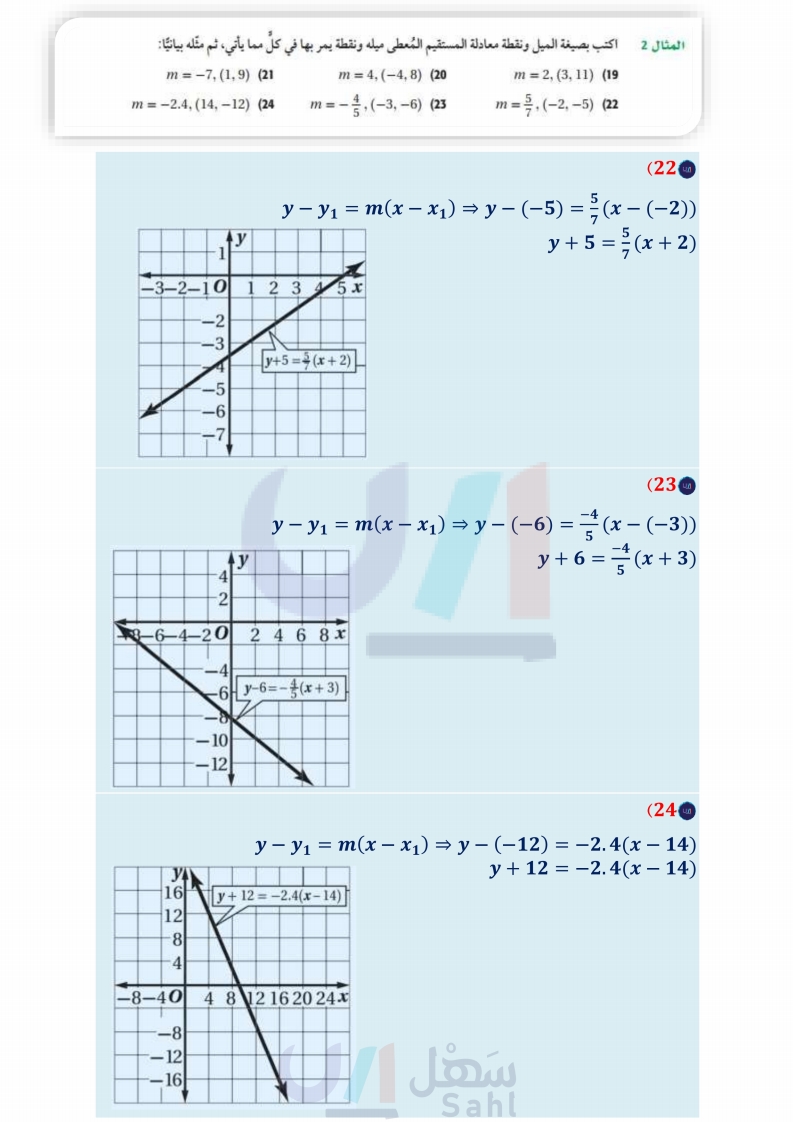
تأكد المثال 1 اكتب بصيغة الميل والمقطع معادلة المستقيم المعطى ميله ومقطع المحور لا له في كل مما يأتي، ثم مثله بيانيا: m = 4, b = -3 (1 : m = }, b = -1 (2 2 - 313, b = 5 (3 2 m = المثال 2 اكتب بصيغة الميل ونقطة معادلة المستقيم المعطى ميله ونقطة يمر بها في كل مما يأتي، ثم مثله بيانيا: m = 5, (3, -2) (4 m = = (-2, -3) (5 - 4.25, (−4, 6) (6 المثالان 34 اكتب بصيغة الميل والمقطع معادلة المستقيم الذي أُعطيت نقطتان يمر بهما في كل مما يأتي: (0, 1), (4, 4) (7 (4,3), (1, −6) (8 - m = - (6,5), (-1,-4) (9 المثال 5 (10) اكتب بصيغة الميل والمقطع معادلة المستقيم العمودي على 6 + 2 = y ، والمار بالنقطة (3). = (11) اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يمر بالنقطة ) ، ويوازي المستقيم الذي معادلته .y = 4x - 5 و المثال 6 (12) عروض يقارن سلمان بین عرضين مقدمين من نادٍ رياضي. يدفع بموجب العرض الأول اشتراكًا شهريًا قدره 100 ريال بالإضافة إلى 10 ريالات عن كل زيارة. ويدفع بموجب العرض الثاني اشتراگا شهريًا قدره 150 ريالا، ويسمح له بعشر زيارات شهريًا. a اكتب معادلة تمثل التكلفة الشهرية لكل من العرضين. مثل كلتا المعادلتين بيانيا. إذا كان سلمان يريد الذهاب إلى النادي 7 مراتٍ شهريًا، فهل يشترك في العرض الأول أم الثاني؟ فسّر إجابتك. J T تدرب وحل المسائل المثال 1 اكتب بصيغة الميل والمقطع معادلة المستقيم المعطى ميله ومقطع المحور لا له في كل مما يأتي، ثم مثله بيانيا : m = 9, b = 2 (15) m = 7,b= -4 (14) - 5 m = (0, -3) (18 m = - 11' 3 4' -1, (0, 4) (17 m = -5. b = -2 (13 m = 12, b = 1 (16 المثال 2 اكتب بصيغة الميل ونقطة معادلة المستقيم المعطى ميله ونقطة يمر بها في كل مما يأتي، ثم مثله بيانيا : m7, (1, 9) (21 (1,9) m4, (-4, 8) (20 m2, (3, 11) (19 m = −2.4, (14, -12) (24 m = - ½½, (−3, −6) (23 5 m = ½, (−2, −5) (22 المثالان 34 اكتب بصيغة الميل والمقطع معادلة المستقيم الذي أعطيت نقطتان يمر بهما في كل مما يأتي: (2,1), (2, 6) (26 (0,5), (3,3) (28 (2, 4), (-4, -11) (30 الدرس - صيغ معادلة المستقيمة الP121 Ministry of Education 2024-1446 (-1,-4), (3,-4) (25 (−3, −2), (−3,4) (27 (-12, −6), (8, 9) (29

تأكد اكتب بصيغة الميل والمقطع معادلة المستقيم المعطى ميله ومقطع المحور y له في كل مما يأتي ثم مثله بيانيا

تأكد اكتب بصيغة الميل والمقطع معادلة المستقيم المعطى ميله ونقطة يمر بها في كل مما يأتي ثم مثله بيانيا

تأكد أكتب بصيغة الميل والمقطع معادلة المستقيم الذي أعطيت نقطتان يمر بهما في كل مما يأتي:

أكتب بصيغة الميل والمقطع معادلة المستقيم العمودي على y=-2x+6

أكتب معادلة تمثل التكلفة الشهرية لكل من العرضين

تدرب اكتب بصيغة الميل والمقطع معادلة المستقيم المعطى ميله ومقطع المحور y له في كل مما يأتي ثم مثله بيانيا

تدرب اكتب بصيغة الميل والمقطع معادلة المستقيم المعطى ميله ونقطة يمر بها في كل مما يأتي ثم مثله بيانيا

تدرب أكتب بصيغة الميل والمقطع معادلة المستقيم الذي أعطيت نقطتان يمر بهما في كل مما يأتي

اكتب بصيغة الميل والمقطع معادلة المستقيم الممثل بيانيا، أو المعطى وصفه في كل مما يأتي: MN (32 EF (31 M 88 У N IM -2 4 +2 8642 E -8-6-4 2468x O -8-6-4 O 2468x F −4 -4 -6 -8 -6 -8 (34) يحوي النقطتين -13-,8-) ,(5- ,4-) (-1,-2), (3, 4) bill (33 35) مقطع المحور x يساوي ،3، ومقطع المحور ا يساوي 2- (36) مقطع المحور x يساوي - -، ومقطع المحور لا يساوي 4 المثال 5 اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يحقق المعطيات في كل مما يأتي : (37 (38 يمر بالنقطة (74) ، ويعامد المستقيم 9 + x ,7)، = يمر بالنقطة (110) ، ويوازي المستقيم 7 = y . 2 (39) يمر بالنقطة (6)، ويوازي المستقيم 1 + y = - x . 3 (40) يمر بالنقطة (2) ، ويعامد المستقيم 8 - y = 5x . المثال 6 (41) جمعية خيرية نظمت جمعية خيرية حفلًا لتكريم مجموعة من حفظة القرآن الكريم، فاستأجرت قاعة لتقيم فيها الحفل. إذا كانت أجرة القاعة 1500 ريال بالإضافة إلى 15.5 ريالًا عن كل شخص يحضر الحفل. a اكتب معادلة تمثل تكلفة استئجار القاعة y إذا حضر x شخصًا. (b) مثل المعادلة بيانيًا. إذا حضر الحفل 285 شخصًا، فكم تكون تكلفة استئجار القاعة؟ d إذا رصدت الجمعية 6000 ريال لاستئجار القاعة، فما عدد الأشخاص الذين يمكن أن يحضروا الحفل ؟ (42) توفير يوفر عبد الله نقودًا ليشتري مذياعًا مرتبطًا بالأقمار الاصطناعية، ويدفع رسوم الاشتراك السنوي بخدمة الأقمار الاصطناعية . فبدأ بتوفير 200 ريال أهديت إليه في عيد الأضحى ، وبعد ذلك كان يضيف 40 ريالًا كل أسبوع . ) اكتب معادلة تمثل ما وفّره عبد الله لا بعد x أسبوعًا. وزارة التعليم Ministry of Education 2024-1446 الربط مع الحياة تصل إشارات بث إذاعة FM إلى km 64 - 48) تقريبا. أما إشارات البث الإذاعي بواسطة الأقمار الاصطناعية فتصل إلى b) مثل المعادلة بيانيا. متى يوفر 500 ريال؟ إذا بدأ التوفير منذ أسبوعين، وكان ثمن المذياع 700 ريال ، ورسم الاشتراك السنوي بخدمة الأقمار الاصطناعية 420 ريالًا ، فمتى يوفر مبلغا يكفي لذلك ؟ فسِّر إجابتك. أكثر من km 35200 استعمل الشكل المجاور لتسمي أي مستقيم يحقق الوصف في كلُّ مما مما يأتي: (43) يوازي المستقيم 3 - y = 2x . . y = 3 x + 7 (44) يعامد المستقيم 7 + x (45) يتقاطع مع المستقيم 5 - y = x ، ولكنه لا يعامده. } q x -1- n У 0 الفصل 2 التوازي والتعامد 122

اكتب بصيغة الميل والمقطع معادلة المستقيم الممثل بيانياً، أو المعطى وصفه في كل مما يأتي

مثال 5اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يحقق المعطيات في كل مما يأتي

اكتب معادلة تمثل تكلفة استئجار القاعة y إذا حضر x شخصا

يوفر عبد الله نقودا ليشتري مذياعا مرتبطا بالأقمار الاصطناعيةاكتب معادلة تمثل ما وفره عبد الله y بعد x اسبوعا

استعمل الشكل المجاور لتسمي أي مستقيم يحقق الوصف في كل مما يأتي

حدد ما إذا كان المستقيمان متوازيين أو متعامدين، أو غير ذلك في كلُّ ممّا يأتي: y = − 1 ½ x - 12, y = 2x+7 (47 y = 2x + 4, y = 2x - 10 (46 y – 3 = 6(x + 2), y + 3 = - 13 (x − 4) (49 y – 4 = 3(x + 5), y + 3 = - 3 (x + 1) (48 3 الربط مع الحياة بعد تشكيل الآنية من الصلصال، يتم إدخالها في أفران خاصة عند درجة حرارة تفوق 500°C . (50) اكتب بصيغة الميل والمقطع معادلة المستقيم الذي يمر بالنقطة (4) ويوازي المستقيم . y − 2 = 3(x+7) (51) اكتب معادلة المستقيم الذي يمر بالنقطة (812) ويعامد المستقيم الذي يمر بالنقطتين (3) (52) صناعة الفخار : نظّمت جمعية حرف يدوية دورة في صناعة الفخار، وكان رسم الاشتراك 150 ريالًا، بحيث يغطي اللوازم والمواد وكيسًا واحدًا من طين الصلصال وكل كيس إضافي يكلف 40 ريالًا . اكتب معادلة تمثل تكلفة الاشتراك وعدد x من الأكياس المستعملة. (53) تمثيلات متعددة : طلب مدير قصر أفراح من بسام أن ينظم وقوف السيارات في أثناء حفل. وقدم له عرضين للأجر؛ أحدهما أن يدفع له 4 ريالات عن كل سيارة، والآخر أن يعطيه أجرًا مقداره 150 ريالا بالإضافة إلى ريالين عن كل سيارة. ( جدوليًا : أنشئ جدولا يبين ما يتقاضاه بسام عن 20، 50، 100 سيارة في كلا العرضين. عدديًا : اكتب معادلة تمثل ما يكسبه بسام من كل عرض. بيانيا : مثل بيانيا كلَّا من معادلتي العرضين. (d تحليليا أيُّ العرضين أكثر كسبًا لبسام إذا كان عدد السيارات 35 سيارة؟ وأيهما أكثر كسبًا لبسام، إذا كان عدد السيارات 80 سيارة؟ وضح إجابتك. لفظيا : اكتب عبارة تصف العرض الأكثر كسبًا لبسام تبعًا لعدد السيارات. ا) منطقيا : إذا كان عدد السيارات 75 سيارةً، فأي العرضين أكثر كسبًا لبسام؟ وضح تبريرك . مسائل مهارات التفكير العليا (54 تحد أوجد قيمة ، بحيث يمر المستقيم العمودي على المستقيم 8 + 2y + 4 = 6x- بالنقطتين . (n, −4), (2, −8) 55 تبرير حدد ما إذا كانت النقاط (226) تقع على استقامة واحدة. برّر إجابتك. (56) مسألة مفتوحة : اكتب معادلات زوجين مختلفين من المستقيمات المتعامدة التي تتقاطع في النقطة .(-3, -7) (57) اكتشف الخطأ كتب كل من راكان وفيصل معادلة مستقيم ميله 5 ، ويمر بالنقطة (2)، أيهما إجابته فیصل y-4=-5(x-(-2)) y-4 =-5(x+2) Y-4 =-5 – 10 y=-5x-6 راکان y-4=-5(x-(-2)) y-4=-5(x+2) صحيحة ؟ وضح تبريرك. (58) اكتب: أيهما أسهل كتابة : معادلة مستقيم بصيغة الميل ونقطة، أم بصيغة الميل والمقطع ؟ الدرس - صيغ معادلة المستقيمة الـ123م Ministry of Education 2024-1446

حدد ما إذا كان المستقيمان متوازيين أو متعامدين أو غير ذلك في كل مما يأتي

أوجد قيمة n بحيث يمر المستقيم العمودي على المستقيم

اكتب معادلة تمثل تكلفة الاشتراك وعدد x من الأكياس المستعملة

أنشئ جدولا يبين ما يتقاضاه بسام عن 20، 50، 100 سيارة في كلا العرضين

حدد ما إذا كانت النقاط تقع على استقامة واحدة برر اجابتك

اكتب معادلات زوجين مختلفين من المستقيمات المتعامدة التي تتقاطع في النقطة (-3،-7)

أيهما إجابته صحيحة ؟ وضح تبريرك

أيهما أسهل كتابة معادلة مستقيم بصيغة الميل ونقطة، أو بصيغة الميل والمقطع؟

A وزارة التعليم Ministry of Education 2024-1446 E تدريب على اختبار معادلة المستقيم الذي يمر بالنقطة (60) أي مما يأتي هي (59) أي مما يأتي هو التمثيل البياني للمستقيم الذي يمر بالنقطة (2) ، ويعامد المستقيم 5 + x (-2, −3) C У A sy = 2 B 54 C 7 8 9 D y = 3x + 7 A y = + x + 7 B 0 x y = y = - = x = -3x - 5 C 1 X 5 D 3 O D У B 0 x مراجعة تراكمية أوجد ميل المستقيم الذي يمر بالنقطتين A,B في كل مما يأتي: (الدرس (4-2) A(4,3), B(5, −2) (61 A(2,5), B(5, 1) (63 A(0, 2), B(-3,-4) (62 أوجد قيمة x, y في كلَّ من الشكلين الآتيين : (الدرس (2-2) (4x-8)° (y²)° 3x 48° (65 (64 (6y+10)° (5x −21)° 4x الشكل المجاور : 26 = 3, °47 = m1 = 58° , m22. أوجد قياس كل من الزوايا الآتية (الدرس (2-2) Z6 (68 29 (71 B 6.x° A 3x° (12y – 10) ° F D E Z5 (67 Z8 (70 Z7 (66 Z4 (69 استعد للدرس اللاحق (72) إذا كان BE AD متعامدتين، فأوجد قيمة كل من x,y , الفصل 2 التوازي والتعامد 124

أي مما يأتي هو التمثيل البياني للمستقيم الذي يمر بالنقطة (-2،-3)

أوجد ميل المستقيم الذي يمر بالنقطتين A, B في كل مما يأتي

إذا كان AD ،BE متعامدين أوجد قيمة كل من x, y

أي مما يأتي هي معادلة المستقيم الذي يمر بالنقطة (1،-2)، ويعامد المستقيم

أوجد قيمة y و x في كل من الشكلين الآتيين

أوجد قياس كل من الزوايا الآتية